Typically in 1st Grade, your child is getting familiar with the concept of addition and subtraction, as well as how to perform these operations. They will start with using their fingers, counting on and then move to more effective strategies.
Addition is the most basic operation that others are based on - and so this is what your child learns first. However, since addition and subtraction are so inter-related, we often look at their strategies together and many foundational fact sets help with improving addition and subtraction speed together.
What are strategies?
Math Fact Strategies are ways kids can simplify an unfriendly problem into a friendly one. Each of the 4 basic operations - addition, subtraction, multiplication and division have strategies. We normally look at strategies in pairs - Addition and subtraction in one pair and Multiplication and division in another pair.
Note that these strategies are not meant to be rote-learnt - they are not procedures that your child needs to adhere to in every condition. Instead, think of them as potential shortcuts your child can take - they need to practice using these strategies, but once they are very familiar with them, the ideal end-goal is for your child to be picking a strategy on the fly that helps them with a particular addition or subtraction problem.
Addition Strategies
Getting fluent in Addition (and Subtraction) can be approached quite methodically. Thanks to Dr. Jennifer Bay-William's work on how to approach Math Fact Fluency, we now know that there is an optimal way to progress from foundational fact sets to derived fact strategies.
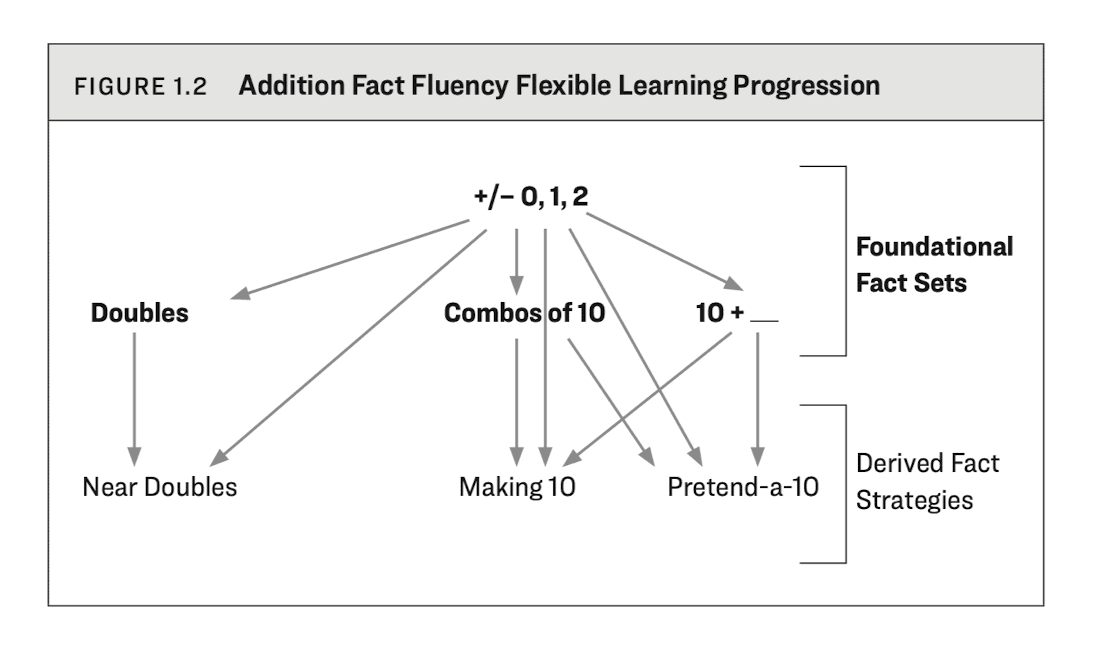
Ref: Math Fact Fluency by Dr. Jennifer Bay-Williams.
Foundational Fact Sets
These are the most basic facts that your child needs to have down.
+/- 0, 1, 2
Basically this involves your child knowing that -
- Adding zero to or Subtracting zero from a number yields the same number
- Adding one to a number yields the next number and subtracting one gets the previous number.
- Adding two can be done by "skip-counting" from the current number. Similarly subtracting two can be done by "reverse-skip-counting" from the current number.
If your child is not yet fluent with these problems (such as 5-2, 6+0, 3+1, etc), then the first step is to give them enough practice with these problems.
Doubles
Once your child is fluent with +/- 0, 1, 2, the next step is to get them comfortable with doubles.
Doubles are easy to practice and can be very helpful as a foundation towards near doubles strategy. At this step, your child needs to know that double of 2 or 2 + 2 is 4, 3 + 3 is 6 and so on till at lest 10 + 10 is 20.
Combos of 10
A parallel step to doubles would be helping your child be comfortable with combos of 10 - i.e. pairs of numbers that add upto 10. 1 and 9, 2 and 8, 3 and 7, and so on.
Just knowing automatically which numbers add upto 10 is foundational - this helps them with Making 10 strategy which in-turn helps simplify a lot of difficult problems into simpler ones.
10 + __
Another step - and a somewhat easier one - is for your child to be automatic with adding 10. This is easier once they see the pattern, but still can need deliberate instruction to get them to see that pattern.
For e.g. 6 + 10 = 16, 10 + 3 = 13 and so on.
This is a super-helpful foundation for the more advanced strategy Pretend-a-10.
Derived Fact Strategies
Now this is where things get somewhat tricky. These are the strategies that sometimes give common core a bad name, if they are taught the wrong way. However, if your child masters them, they can be incredibly powerful and help your child develop a strong feel for how numbers work.
Near Doubles
This strategy combines the knowledge of Doubles and +/- 1,2 foundational fact sets.
How would your child put the near doubles in practice?
Let's say they have to do 4 + 5. In this case, they already know 4 + 4 is 8 and should thereby derive that 4 + 5 is 1 more than 8 - which is 9. Same with something like 3 + 5 (2 more than 6) or 8 + 9 (1 more than 16).
They could also approach the problems from the other end - 3 + 5 is "2 less than double of 5" or 8 + 9 is "1 less than double of 9".
You can see how being automatic with doubles by this stage is super critical. If they can understand the logic of near doubles but are not yet automatic with doubles, the strategy can actually slow them down compared to some other more basic strategies.
Making 10
Making 10 is another advanced strategy that relies on 3 foundational fact sets - (1) Combos of 10 (2) +/- 1,2 and (3) 10 + __. This is mainly useful when one added is close to 10.
Let's say the problem is 9 + 5. Now they know that 9 + 1 = 10. So using this knowledge, they can visually imagine 1 moving from 5 to 9, leaving the problem as 10 + 4.
This makes the problem much friendlier, and since they are also automatic with 10+___, the answer can come out instantaneously.
When we try to write down this logic, it might seem counter-productive - indeed there are many memes about this "new math" that is more steps compared to the "old math". But if you are doing this intuitively, and you are automatic with the foundational fact sets, these derived fact strategies are actually way more powerful to do math mentally.
Pretend-a-10
Pretend-a-10 is a very similar strategy to making 10, but it has a subtle difference. It again relies on all 3 foundational fact sets, but is slightly more difficult than Making 10.
Let's take the same problem - 9 + 5.
Here, the child will first pretend that the problem is 10 + 5 - and get 15. Then they will remember that the first added they used was actually 1 more than 9 - and so for the correct answer to 9 + 5, they have to reduce 1 from 15. Which gives them 14.
How to Teach your Child these Strategies?
This is a very good question. Ideally, your child's teacher is trained in this. If not, the book from Dr. Jennifer Bay-Williams is excellent, since it goes step by step for each fact set, and also suggests a lot of practice games to help the kids get really good at it.
The techniques involve providing visual cues to kids so they can understand how the strategies actually work, helping them do the operations in different ways (ten-frames, number line, cuisenaire rods), Number Talks, and also a lot of fun practice.
You can also look at the companion website for the book which is a fantastic resource for parents and teachers.

Ref: Math Fact Fluency by Dr. Jennifer Bay-Williams.
This does require a significant amount of time though, from you as a parent, to learn about the pedagogy and then help your child build these skills slowly and methodically.
Another, simpler way, could be to just try out Monster Math.
Monster Math is built on Dr. Bay-William's research and also provides a lot of visual, fun, practice. It also has the added advantage of being designed as a real game - so your child actually has as much fun as they have when playing a game they like. It also comes with a 7-day Free trial, so try it now!


