Multiplication and especially Division is where Math starts getting harder for a lot of kids. Kids start seeing Multiplication as repeated addition sometimes in 2nd Grade itself, but it's in the 3rd Grade that they typically have to start getting their Multiplication facts down.
What are strategies?
Math Fact Strategies help kids simplify an unfriendly problem into a friendly one. Each of the 4 basic operations - addition, subtraction, multiplication and division can have strategies. We normally look at strategies in pairs - Addition and subtraction in one pair and Multiplication and division in another pair.
These strategies are not meant to be rote-learnt as procedures. Instead, they are more about understanding the properties of the operations so well, that they can instinctively make unfriendly problems friendly and then maybe even solve it mentally.
Multiplication Strategies
Getting fluent in Multiplication and Division can follow a very different path to what is traditionally done.
Traditionally, we have been making kids rote-learn tables of 1 to 10 (sometimes upto 12, or even 15). They generally do it with the help of a multiplication songs or multiplication charts. While this is helpful to see patterns and can help - it can also hamper your child's progress if they are not good at memorising facts.
A different progression can look like below -
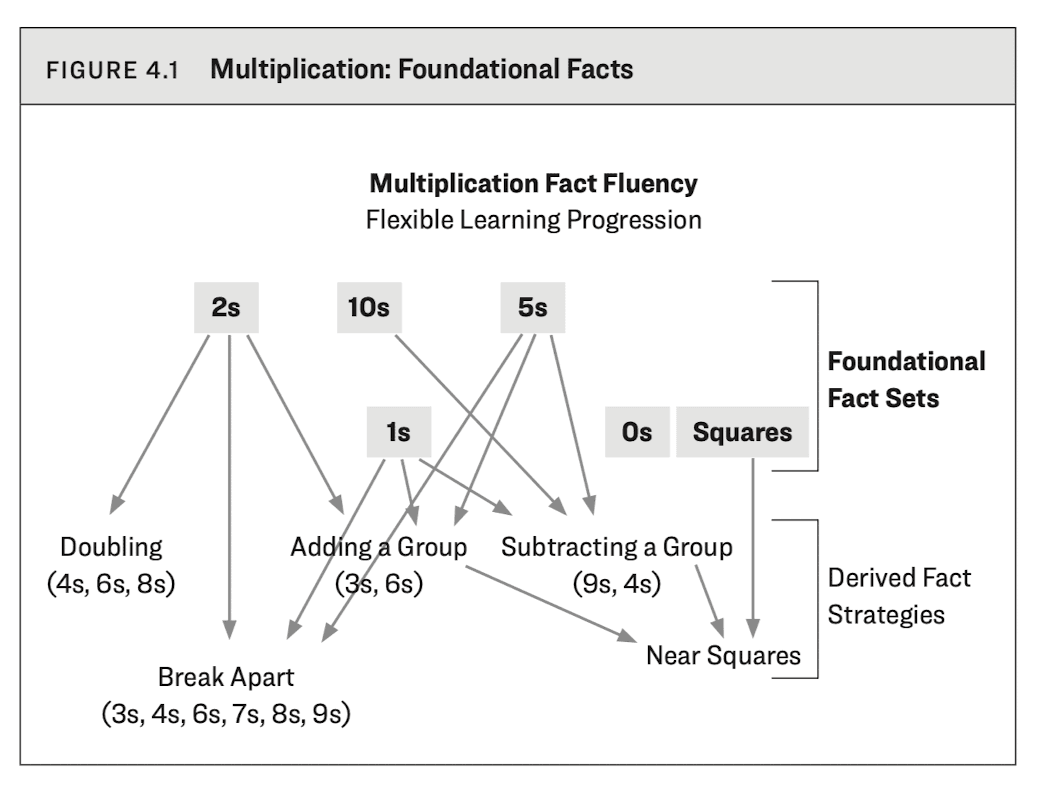
Ref: Math Fact Fluency by Dr. Jennifer Bay-Williams.
Note that this assumes fluency with addition and subtraction fact strategies. If your child is yet to be fluent with that, I would recommend to start with that, even if it seems a grade level or two below where your child is. This going back one step can save a lot of time and heartache by the time they come back to multiplication and division.
Foundational Fact Sets
Instead of 1 to 12, you can start with the basic multiplication tables that are also easier to learn and lend to a certain pattern.
2s, 10s, and then 5s
These are the easiest to learn. 2s are a step up from skip counting, 10s are an intuitive pattern (5 X 10 = 50, for e.g.). 5s are a bit harder, but still easier than a lot of other multiplication facts.
0s and 1s
These are not difficult to know the answer - but they are difficult to understand conceptually, so deserve some time on it's own. They also generally can make a child think (for e.g. a multiplication product is higher than the multiplicands, but when you multiply by 0 or 1, it's not true).
Knowing that multiplying something by zero is zero - and why - is crucial. Similarly visually understanding why multiplying by 1 leads to the same number is important.
Squares
This is a good intermediate step before going to the harder facts. These have generally been skipped in the traditional multiplication instruction, but can be very useful to know.
Squares are just knowing that 2 x 2 = 4, 3 x 3 = 9 and so on, till 10. These might need some memorising - even after the child understands the concept. But this is worth it, because once your child knows squares, they can easily derive a whole lot of multiplication facts using the "near squares" derived strategy.
.
It might seem like foundational facts are very few, but they actually cover most of the multiplication facts - especially when used with the commutative property (i.e. 2 x 4 is same as 4 x 2).
Visualising this is easier than explaining in words -
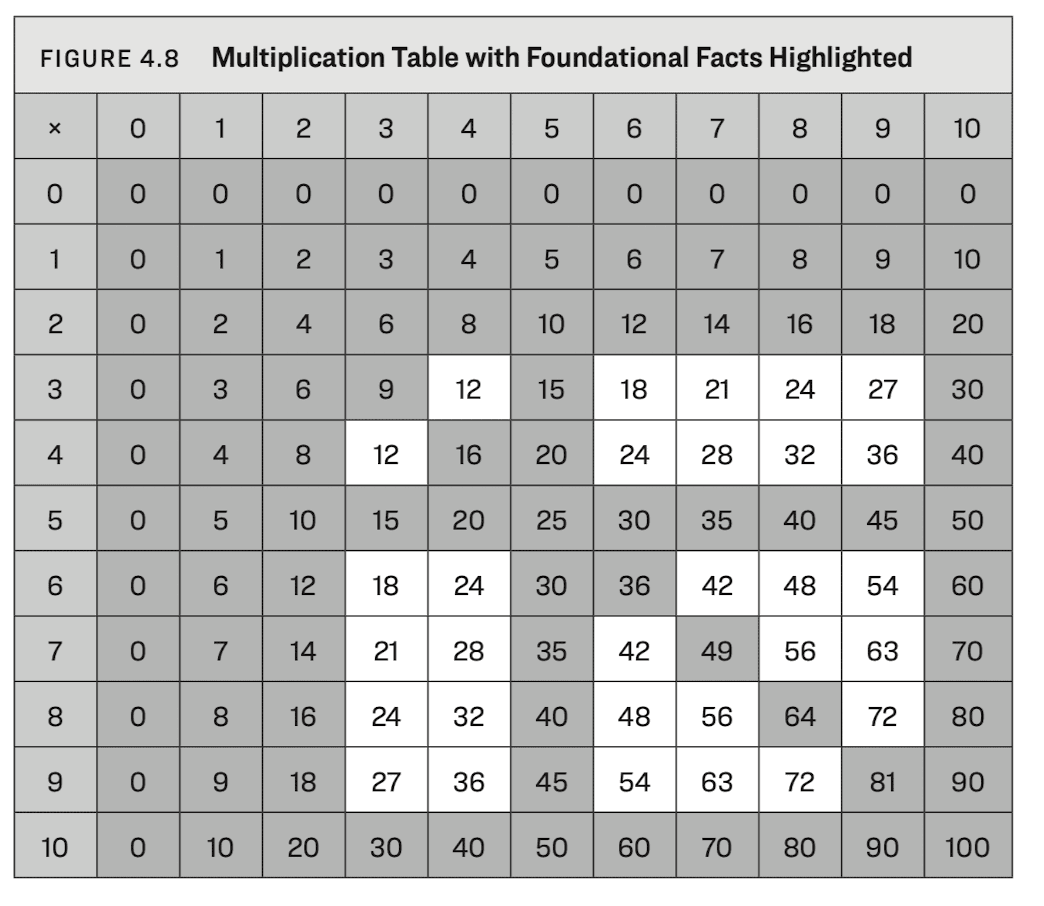
Ref: Math Fact Fluency by Dr. Jennifer Bay-Williams.
Derived Multiplication Strategies
Now this is where things get interesting. We are not yet going to multi-digit multiplication - instead, we are looking at the difficult fact sets, such as facts of 4, 6, 8 and then the most difficult ones - 3s, 7s, 9s.
These strategies require the child to be automatic with the foundational strategies, so only get here once they are truly fluent in the foundational facts above. Time spent on achieving that is worth it, because it can make learning and using derived facts that much easier.
Doubling
If your child has some of the additional foundational fact strategies down, they should be very comfortable with doubling by now. And with the foundational multiplication facts down, combining these two skills can allow them to derive multiplication problems involving 4s and 8s. (and even 6s, once they are comfortable with 3s).
For example, facts involving 4 are a double of the same fact where the 4 is replaced by 2.
for e.g. 4 x 6 is nothing but double of 2 x 6 - so double of 12 = 24.
8 is similar but it's a double of facts of 4. If you are starting from facts of 2, it's doubling it twice.
So 8 x 3 is nothing but 2 x 3 doubled twice - 6 doubled to 12 doubled to 24.
As you might notice, your child does need to know doubles for much bigger range of numbers for this to work - as the facts get higher. For e.g. for 8 x 8, they might have to start with 2 x 8 = 16, and then double that twice (to 32 and 64) which is quite hard.
So it is advisable to limit this strategy to facts where the second multiplicand is under 7 or so and use other strategies when they are easier. This is also an example why strategies are not procedures - your child needs to choose them on the basis of what makes the solution simpler based on how many doubles they know; and if it will make the solution harder (because they don't know the doubles for that yet) then rely on a different strategy.
Adding a Group
This is a very useful strategy in a wide variety of situations, and goes to the core of understanding what multiplication is.
Since multiplying is nothing but repeated addition of groups, this strategy relies on child visually understanding it and then using it to derive harder facts from easier ones.
For example, 3 x 6 is nothing but 2 x 6 + 6. That means if you know facts with 2, you can easily derive facts of 3.
Similarly, from Facts of 5 and 10, you can derive facts of 6 and even 11.
6 x 8 = 5 x 8 + 8 = 48.
Subtracting a Group
This further builds on multiplication as repeated addition of groups - but goes the other way. This makes deriving facts of 4 and 9 easy from facts of 5 and 10.
4 x 6 = 5 x 6 - 6 = 24.
9 X 3 = 10 x 3 - 3 = 27.
This is a harder strategy than adding a group, because as numbers grow bigger, subtracting these numbers mentally could get harder.
Near Squares
Now this is a super helpful strategy when the fact in question is close to a square. This uses both the squares facts that your child has hopefully memorised by now, and adding/subtracting a group.
For example, 9 x 8 = 9 x 9 - 9 = 81 - 9 = 72.
Note that to do 81 - 9, they might use the subtracting strategy of making 10, to make it 82 - 10. Math Fact Strategies really build on each other!
Break Apart
Break Apart is the hardest of the strategies and is generally the last to master. Indeed all other derived strategies are special cases of Break-apart - it's also much harder to learn, so it helps to master all other strategies and then come here.
Once your child is familiar with break-apart though, they will be way more comfortable with multiplication in general.
For e.g. - 8 x 9 is the same as 8 x 5 + 8 x 4
It's much better to do this visually -

Division Strategy
The main strategy for division is "Think Multiplication".
Once your child is comfortable with Division, it's best for them to start thinking of the division problem as identifying the right multiplication fact that leads to that dividend (i.e. the number being divided).
So for e.g.
For 20 ÷ 4 - your child will think "4 X ___ = 20" - and then "4 x 5 = 20" so "20 ÷ 4 = 5".
So their division comfort will be directly a result of comfort with multiplication.
How to Teach Your Child these Strategies?
Ideally, your child's teacher is trained in this. If not, the book from Dr. Jennifer Bay-Williams is excellent, since it goes step by step for each fact set, and also suggests a lot of practice games to help the kids get really good at it.
The techniques involve providing visual cues to kids so they can understand how the strategies actually work, helping them do the operations in different ways - visualising multiplication as arrays, groups


